Issues

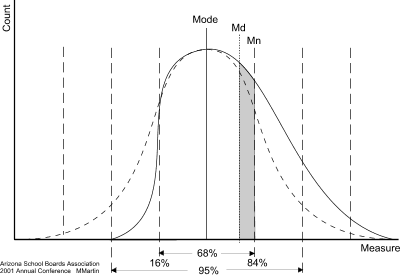
Martin's Paradox

by Michael T. Martin

A fundamental paradox is created by the statistical procedures used in standardizing high-stakes tests that renders them meaningless. What I shamelessly name "Martin's Paradox" makes it mathematically certain that the better your schools perform, the worse they will look on high-stakes evaluations.

This is counter-intuitive, as is clear from the popular radio fantasy regarding the news from a mythically rural community known as Lake Woebegone "where all of the children score above average" on school tests. The idea that all the children would score above average is a humorous fantasy, but most people do not realize that it is statistically backwards.

In reality, once you understand Martin's Paradox you realize that the better your educational system, the more your students will score BELOW average. It is a mathematical certainty, once you understand the paradox. Lake Woebegone is actually a very inferior town.

The confusion arises because most people, including most experts, assume that test scores form statistical bell curves, and therefore when students learn more, the bell curve simply moves to a higher average. Unfortunately, this cannot happen because nearly all high-stakes tests are "standardized."

The first step of standardization is to set the average to some pre-arranged "standard" score (typically 500 as with the SAT and Arizona's AIMS tests). Then all of the actual individual scores are arranged proportionally around the standard based on their relationship to the original average. As a consequence, the average score can never shift, it is always set to the predetermined standard.

The problem is that good schools change the shape of the normal bell-curve. A normal bell-curve has a mean (the average) and median (the middle score) in the center of a peak (the mode), and two-thirds of all student scores will be found between the shoulders of this peak. The other third will be on either side of those shoulders, where the bell-curve plunges into two flaring "tails." When a school is successful in educating students, the lower tail is diminished and the upper tail bulges with students scoring higher. The distribution of scores no longer looks like a bell. Instead it has the shape of a human "nose," known as a "skewed normal" distribution (see illustration below).

Consider a hypothetical school where each year the 8th-grade students take the same test. The school governing board decides to provide remedial help to all students who score in the lower tail and a gifted program for all students who score in the upper tail. In prior years, the scores formed a normal bell-curve distribution.

For illustration purposes, in each of the next five years, the two-thirds of the 8th-grade students in the peak of the bell curve have exactly the same scores as those 8th-grade students in the peak of the prior years. But each year, the number of students in the lower tail declines because of the remedial program until only two percent of the students score there, while each year the number of students in the upper tail increases until 30 percent of the students score there.

Most everyone would consider this a successful program: we have boosted our weaker students and our best students excelled. Even though two-thirds of the 8th-grade students in the school scored exactly the same every year, the lower tail essentially disappeared, while the upper tail bulged: the classic "nose" shape of the "skewed normal" distribution.

The "mode" in this graph is the mode for both the dashed bell curve and the solid skewed normal distribution of test scores. The dashed vertical lines represent the three standard deviations above and below the dashed bell curve's mode/mean/median. However, the skewed distribution has a different mean (Mn) and median (Md). All of the scores between this new mean and the mode are scores that formerly would have been above average, but are now below average because the average increased even though all of the scores within one standard deviation of the mode (the old mean) have not changed.

However, in a skewed normal distribution, the mean and median are no longer found at the peak of the bell-curve. Both move onto the bridge of the nose, with the median lagging about a third of the way behind the mean (this relationship is so well known it is listed in almost all statistics textbooks as the "empirical formula" for finding the mode). Even though the overall average increases, the process of standardizing scores always sets the mean to the standard.

Consequently, a large number of student scores will fall between the median and the mean where previously there were none (the shaded area in the graph above). It is a mathematical certainty that the more you reduce the number of students in the lower tail by raising their scores, this will raise the overall average, and the more you increase the number of students in the upper tail by raising their scores, this will also raise the overall average, if either or both happen then the more that your students will score below average.

There are actually two separate effects at work here. First, consider the plight of those students who formerly scored in the area above the mode but below the first standard deviation (the upper half of the peak). These students scored exactly the same score that would have made them above average in the past, but now they are counted as scoring below average.

Second, consider the group as a whole. Formerly only 50% of the students scored below average, but now 84% of the students score below average, even though every single student had either the same or a higher score than before!

Since this higher mean is still set to the same pre-arranged standard and the rest of the scores are arranged in relation to this mean, the farther the mean moves onto the nose, the farther each of the individual scores will be shifted to lower standardized scores.

The effect of this shifting from a bell to a nose on standardized scores is that the two-thirds of the students who scored exactly the same each year will have lower and lower standardized scores. Thus it is a mathematical certainty that the better your educational system, the more your students will score below average.

Even if every single student in every school had higher scores every year, it will not change the fact that removing students from the lower tail and adding students to the upper tail will cause the standardized scores of your students to decline each year. Mathematically, there is no escaping Martin's Paradox: the better your educational system, the more your students will score below average, and the farther their standardized scores will decline.

The supposed salutary state of the Lake Woebegone students is entirely backwards: the more students score above average, the worse your school system is. The better your educational system, the more your students will score BELOW average. It is Martin's Paradox. But is this all theoretical foofaraw (there is actually such a word)? Well, let's take a look at an example from Arizona's high-stakes AIMS test.

Next issue: Martin's Comparadox!