Issues

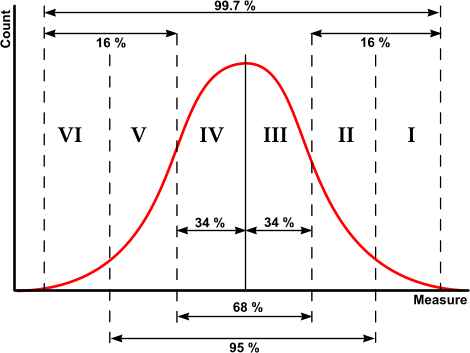
Data numbers are different than regular numbers. Numbers that come from measurements (i.e. data) are different than numbers that come from counting. The numbers that are developed from measurement don't provide any real information individually.

Just because two data numbers (measurements) are different does not mean one is larger than the other. This reality needs to be understood before data are used for decision making. Only when numbers are analyzed using the bell curve can they provide any real information. The bell curve carries the secret to understanding data.

The bell curve represents an idealized version of the measurements that one collects about some phenomenon. It is idealized because the bell curve represents the mathematical formula that has been found to closely match the random variation that occurs when measurements are made.

Whenever we collect data it consists of numbers that are the "observed" values of some underlying "true" value that we are actually trying to measure. We really don't care about the measurements, the data numbers individually have no value. What we want is the "true" value we are trying to measure.

There will be variation in those observed numbers that typically produces a cluster around some central value. We can take the average of these numbers to find the "mean" which we assume is somewhere close to the unseen true value.

The mean is not the true value, we just assume that the true value exists somewhere near the mean. This is critical in understanding data and how it differs from regular numbers. Data is understood to be wrong: the individual measurements are not the true value.

If you do not understand that data is always wrong, you cannot really interpret data. All measurements, including test scores, represent numbers that by definition are wrong: they are not the true value.

A rule of thumb is that most measurements are fairly close to the mean, and thus close to the true value, but there will be a few values that differ by a large amount. However, these large differences will be infrequent while most measurements have small differences.

This is reflected in the shape of the bell curve: there are a lot of measurements clustered around the central value of the mean but the number of measurements declines rapidly for values the farther they are from the mean. The value of the bell curve is that it mathematically tells us how likely some observed value is to be the true value.

However, it is crucial to recognize that even when carefully measuring the same underlying value, normal variation could result in one observed value varying below the mean while another varies above the mean. Both observed values represent the same underlying "true" value but differ only because of "normal" variation.

Too many people fail to recognize that when obtaining data we are after the true value, the observed values have no real import individually. It is only when we consider several observed values that we can get an idea of how they relate to the true value. Thus we need to adjust observed values to account for normal variation.

To try and estimate normal variation, a mathematical formula called the "Standard deviation" uses the squared differences between the average (i.e. mean) of all of our collected measurements and each individual measurement to determine how our values fit into a bell curve.

We use this odd formula of squared deviations because it turns out that the formula for the standard deviation mathematically works with the mathematical formula for the bell curve so that 6 standard deviations, 3 above and 3 below the mean, will mathematically include 99.7 percent of all our measurements. The standard deviation is often referred to by the Greek letter sigma, and thus the width of the normal bell curve, meaning 99.7 percent of all our measurements, is 6 sigma.

This means that with normal variation there are six equal spans of measurement, a standard deviation wide, across the bell curve from tail to tail: 3 above and 3 below the mean. Those spans are equal width but the number of measurements in each span varies radically since the number of measurements forms a peak near the mean but declines rapidly the farther the measure is from the mean.

Some of our normal measurements may be farther from the mean than 3 standard deviations, but overall there should only be 3 of those outliers in every 1,000 measurements (99.7% of a thousand are in the 6 sigma). Therefore all data values within 3 standard deviations of the mean could be equivalent, differing only by normal variation.

All this technical gobbly-gook simply means that we know each of our measurements is wrong, but the bell curve can tell how much they are wrong. More importantly, it can tell us whether any individual measurement is really different from the other measurements. Just because two data values are different doesn't say anything unless one or the other is more than 3 standard deviations from the mean.

When we collect data we rarely have the opportunity to collect the millions of data points that could be collected to form an actual bell curve, so we use the mathematical bell curve to represent what we would expect to collect from extensive data measurements and compare it assuming the mean and standard deviation of our "sample" data will be similar to what we would find if we had a large number of measurements.

If we assume that the data we collect includes "normal" variation within a bell curve, the mathematics tell us that 99.7 percent of our measurements will be within three standard deviations from the mean. But that also means that even when our mean is actually very close to the underlying "true" value, we can expect to observe measurements as far as 3 standard deviations from the mean that actually are just normal variation of the measuring process for that true value.

Also, the mathematics suggest that just over a third (34%) of the measurements we make will be within one standard deviation of the mean, which in turn means that over two-thirds (68%) of all the measurements we make will be within the two standard deviations on either side of the mean. And ipso facto the remaining 32 percent will consist of 16 percent above and 16 percent below that center two standard deviations.

What this means, in reality, is that if you test 1,000 students at some grade level in some subject, even if every student has the same underlying knowledge, you can expect students to have test scores that vary across 6 standard deviations because of normal variation. It is only because of variation in our test construction, classroom variations, and other factors such as illness and anxiety, that the students with identical knowledge receive different test scores.

As a consequence, when you are presented with a list of test scores ranked from high to low, there may be absolutely no difference in the actual true knowledge possessed by any of those students if those scores are all within 3 standard deviations of the mean.

Only those students whose scores were more than 3 standard deviations from the mean can be said to different from the other student scores. All of the other student scores cannot be said to be different, whether they have actually scored above or below average, because all of the scores within the 6 standard deviations of normal variation are equivalent in reality to the same underlying true value.

If you say that student A has a higher test score than student B, then you may be literally correct but essentially wrong if you mean that student A knows more than student B. If both students scored within 3 standard deviations of the mean, then their actual knowledge is the same.

Statistical variation from all its sources means that any number you are given as a measurement is simply a token for some underlying true value. When you measure anything, you are trying to get the "true" value but what you actually get is the "observed" value and multiple observed values of the same true value will normally vary by 6 standard deviations. All of those observed values are exactly equivalent to each other in terms of the underlying true value.

In other words, there is no basis in reality for considering the true value of these scores to be different, they differ only because of normal variation in measurement, or as it is sometimes called: "measurement error". The fact that two students have widely different test scores may mean nothing, both may have exactly the same level of knowledge that the test measures but with different measurement variation levels.

This is true for all measurements in any endeavor. Data numbers are different from other numbers, they are not really a point on a graph, but actually are more like a disc with a 3 sigma radius around the mean value. You cannot say that two numbers are different unless they belong to different clusters: meaning that one number belongs to one bell curve but the other number is more than 3 standard deviations away from the mean of that bell curve. Even then, there is a 3 out of a thousand chance the two are the same.